Benoît Gibson
Alors que les compositeurs comme Boulez ou Stockhausen développent leurs méthodes compositionnelles à partir de techniques sérielles, Xenakis suit des critères autres que ceux issus de la tradition musicale. En abordant le phénomène musical globalement, il découvre un monde sonore qui inclue des textures comparables aux phénomènes naturels dont l’organisation semble soumise à la loi des grands nombres. Cependant, bien que Xenakis critique la musique sérielle (1994, 39-43), il ne la rejette pas complètement. Dans la section centrale de Metastaseis (1954), sa première œuvre importante, il expérimente des processus sériels (cf. Barthel-Calvet 2003). Mais il ne s’accommode pas des principes sériels dont il critique les limites restrictives. En s’opposant à ces limites, il développe l’idée de l’indéterminisme comme principe d’organisation des composantes du son. En admettant l’indépendance totale des sons, Xenakis pouvait les soumettre aux lois du hasard et créer des sonorités inouïes. Pour cela, il lui fallait un nouvel outil. Xenakis s’inspire de la théorie des probabilités.
L’existence de différentes lois de probabilité correspondant à différents types de « masse » a été une révélation pour Xenakis qui a introduit dans sa musique celles auxquelles il pouvait soumettre les composantes du son. Contrairement aux principes sériels, le recours au calcul des probabilités n’imposa pas de limite au nombre de sons qu’il voulait utiliser, mais les organisa selon une logique de distribution pour laquelle il fallait définir une moyenne ou une densité. Ainsi, l’intervalle, la durée, l’intensité́, etc. deviennent des variables dont les valeurs peuvent être définies ou évaluées par rapport à une distribution théorique. Xenakis élabore deux types de musique stochastique : la musique stochastique libre, qui concerne les œuvres des années 1955-57 ; et la musique stochastique markovienne, qui s’applique aux œuvres des deux années suivantes : 1958-59.
Le premier texte de Xenakis qui expose des applications possibles de la théorie des probabilités pour organiser les composantes du son date de 1956. Il inclut des exemples qui traitent des vitesses, des durées et des intervalles de hauteur. Les deux premiers seront examinés ici. Le glissando joue un rôle essentiel dans la musique de Xenakis. Il s’assimile à une droite dont la pente correspond à une vitesse. Pour illustrer une application possible de la théorie des probabilités à la distribution de vitesses, Xenakis fournit un exemple tiré des mesures 52-59 de Pithoprakta (1955-56), accompagné d’une représentation graphique de ces mesures réalisée sur du papier millimétré.
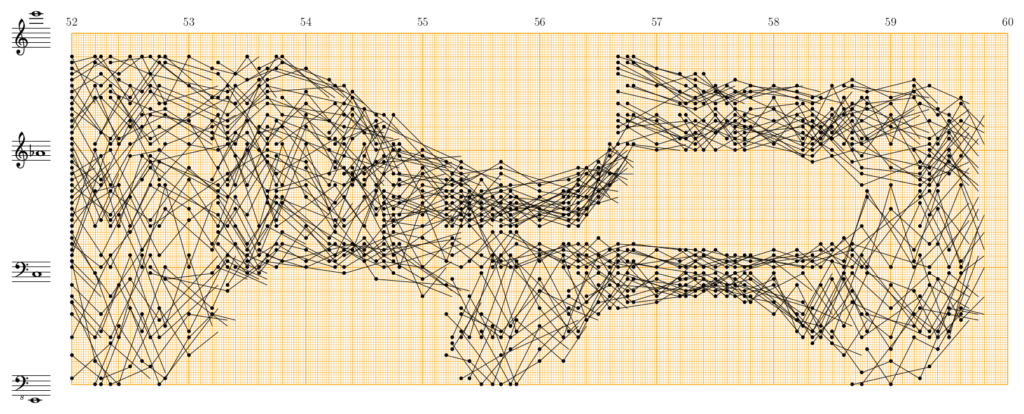
Transcription à partir de la partition : Benoît Gibson.
Dans ce passage, chaque glissando est déclenché par un pizzicato. L’arrivée d’un glissando ne correspond pas nécessairement au départ du suivant : Xenakis brise les lignes afin de les déplacer dans différents registres. En faisant cela, il prend soin de noter la corde sur laquelle s’effectue chaque glissando et s’assure, lors d’un changement de corde, que l’instrumentiste garde la même position. La forme de ce nuage est limitée par les registres instrumentaux et le choix d’une densité constante. Au départ les glissandi occupent l’espace dans les limites des possibilités instrumentales. Puis Xenakis module la sonorité en lui soustrayant des zones de registre et mettant en relief des régions densifiées. Tel un sculpteur, il modifie les caractéristiques sonores de la texture. Cependant, les transformations de ce nuage sonore abritent des calculs. Xenakis résume comme suit les principes théoriques à l’origine de ce passage :
Chacune des droites représente une vitesse tirée du tableau de probabilités calculées avec la formule :
$$f(v) = \frac{2}{\alpha \sqrt[]\pi}e^{-(\frac{v^2}{\alpha^2})}$$
Ont été calculées et dessinées pour ce passage, de la mesure 52 à la mesure 60 d’une durée de 18,5 sec, un total de 1142 vitesses : distribuées d’après la loi de Gauss en 58 valeurs distinctes. La distribution est gaussienne, mais la forme géométrique est une modulation plastique de la matière sonore.
Xenakis 1992, 15
Quinze ans après avoir complété Pithoprakta, Xenakis utilise des passages de glissandi des mesures 52-59 dans Aroura (1971). Comme cela se produit souvent dans ses premières œuvres, il attribue à chaque instrument une structure rythmique basée sur la subdivision de l’unité de temps par 3, 4 ou 5. Xenakis superpose ces valeurs rythmiques pour créer une sensation de continuité.
Dans la foulée de Pithoprakta, Xenakis développe l’idée d’un indéterminisme total. « Quel est le minimum de contraintes logiques nécessaires à la fabrication d’un processus musical ? » (Xenakis 1963, 33). On peut définir le hasard comme une loi esthétique, une philosophie normale (Xenakis 1963, 37). Ainsi l’œuvre devient fragment d’une répartition stochastique des événements sonores. Par l’indéterminisme de ses rapports et l’absence d’évolution dynamique, Achorripsis ouvre une nouvelle catégorie que Xenakis nommera « hors-temps ». L’œuvre a pour fondement des distributions d’événements sonores, établies sans égard au temps qui les réalise. Dans l’exemple du nuage des mesures 52 à 59 de Pithoprakta, l’usage du calcul des probabilités ne concernait qu’un seul paramètre : les vitesses des glissandos ; dans Achorripsis, Xenakis généralise l’utilisation du calcul des probabilités en l’appliquant à d’autres composantes du son. Outre les vitesses, les densités, les intervalles de durée et de hauteur, la structure de l’œuvre, se soumet aux lois du hasard. Pour Achorrispis, Xenakis a calculé la probabilité d’occurrence des événements sonores en utilisant la distribution de Poisson :
La musique stochastique markovienne s’inspire de la théorie des événements en chaîne de Markov, où la probabilité de chaque événement dépend de l’état de l’événement précédent.
Malgré la place qu’occupe la musique stochastique markovienne dans les écrits théoriques de Xenakis, soit près du tiers de la première édition de Musiques formelles (Xenakis 1963, 61-131), trois œuvres seulement y font référence explicitement : Analogique A, Analogique B et Syrmos. Xenakis compose Analogique A pour neuf instruments à cordes (trois violons, trois violoncelles et trois contrebasses) en 1958, un an après avoir terminé Achorripsis. Dans Analogique A, il part de l’hypothèse que tout son est une intégration de grains (Xenakis 1963, 61 ; voir aussi la Synthèse granulaire) pour définir un ensemble de huit trames différenciées et identifiés par les lettres de (A) à (H). Ce que Xenakis nomme « trames », ce sont des petits nuages d’une durée d’une demi-mesure, caractérisés par la disposition des sons dans les registres, leur densité moyenne et leur intensité. Les trames ainsi définies sont hors-temps. La durée n’est plus une variable associée à une distribution de probabilité. Les modes de jeu arco, sul ponticello, frappé col legno et l’emploi de la sourdine sont utilisés pour modifier le timbre des classes instrumentales. Quant à la disposition des sons dans les registres, elle relève probablement d’une démarche intuitive. Après qu’il a établi une distinction entre les trames, Xenakis définit un processus pour déterminer les probabilités qu’on les trames de se transformer en d’autres trames. La répétition du processus un certain nombre de fois engendre un état d’équilibre avec des proportions fixes pour chacune des trames. Par exemple, les mesures 15-30 d’Analogique A ne contiennent que des trames (A). À l’étape suivante, mesures 31-45, la proportion de trames sera modifiée de façon à contenir toutes les trames.
Les premiers exemples de musique stochastique préconisaient les transformations continues ou explosives de « masses » sonores. Ces transformations prenaient forme dans le temps, elles dépendaient du temps. Puis, à mesure que Xenakis avance dans son projet de formalisation de la musique, il soustrait la définition des êtres sonores à l’emprise du temps. Dans Achorripsis, par exemple, la distribution des durées n’est pas calculée pour chaque instrument, mais de telle sorte que la projection sur une droite des dates de départ définisse un ensemble de valeurs conçu en fonction d’une distribution stochastique. Il en va de même pour les hauteurs : la distribution des intervalles ne s’effectue pas à l’intérieur d’une voix, mais entre les instruments. Il ne s’agit pas d’une superposition de lignes indépendantes, mais d’un nuage de sons conçu dans sa globalité. Xenakis compose des échantillons d’événements sonores qualifiés « hors-temps ». Ces événements sonores sont représentés au sein d’un schéma qui pose l’équivalence formelle entre toutes les occurrences du même timbre instrumental. C’est pourquoi l’organisation stochastique de cette forme admet une mobilité des unités structurelles : sous certaines conditions, les lignes et les colonnes qui constituent la matrice d’Achorripsis sont interchangeables (Xenakis, 1963, 41). La musique ne suit plus un mouvement directionnel : elle ne se dirige pas vers un but. Le même principe s’applique également à la musique stochastique markovienne. Le schéma formel d’Analogique A repose sur des séquences de « trames » définies selon des caractéristiques de densité, de registre et de nuances. Ces trames s’enchaînent selon des proportions inspirées par la théorie des événements en chaîne de Markov. À l’intérieur d’une séquence, une trame peut être remplacée par une autre trame du même type.
Rappelons que Xenakis s’opposa à une conception linéaire des « masses » sonores lorsqu’il critiqua ce qu’il appelait la « polyphonie linéaire » de la musique sérielle dont le résultat n’est « qu’amas de notes à des registres variés » (Xenakis 1963, 18) ; et que pour résoudre cette contradiction, il composa des nuages de sons indépendants : ce qui compte, c’est la moyenne statistique des sons.
Remarques
Texte issu et traduit part Benoît Gibson, 2011. The Instrumental Music of Iannis Xenakis: Theory, Practice, Self-Borrowing. Iannis Xenakis Series, No. 3. Hillsdale, N.Y. : Pendragon.
Références
Barthel-Calvet, Anne-Sylvie. 2003. “MÉTASTASSIS-Analyse : Un texte inédit de Iannis Xenakis sur Metastasis,” Revue de Musicologie 89/1, 129–187.
Xenakis, Iannis. 1956. “Wahrscheinlichkeitstheorie und Musik,” Gravesaner Blätter 6, 28–34.
Xenakis, Iannis. 1992. Formalized Music: Thought and Mathematics in Composition. Rev. ed. Stuyvesant, NY: Pendragon.
Xenakis, Iannis. 1994. “La crise de la musique sérielle.” In Kéleütha (Ecrits), edited by Alain Galliari, preface by Benoît Gibson, Paris: L’Arche.
Citer cet article
GIBSON, Benoît. 2023. “Musique stochastique.” Dans A Xenakis Dictionary, édité by Dimitris Exarchos. https://www.iannis-xenakis.org/en/stochastic-music

