Benoît Gibson
While avant-garde composers such as Boulez or Stockhausen developed their compositional methods on the basis of serial techniques, Xenakis followed criteria other than those stemming from any musical tradition. By approaching the musical phenomena globally, he opened up a new sound world that included textures comparable to natural phenomena governed by the law of large numbers. Despite his criticism of serial music (1994, 39-43), Xenakis did not outrightly reject it. In the middle section of Metastaseis (1954), his first major work, he experimented with serial procedures (see Barthel-Calvet 2003). But he could not adapt to serial principles. He considered them too restrictive. What Xenakis objected to was the limit inherent in serial practice; in response to these limitations, he developed the idea of indeterminism as the principle to organize sound characteristics. By making sounds fully independent, Xenakis could subject them to laws of chance and create sonorities novel to our ears. To achieve this, he would have recourse to other means. Xenakis was inspired by probability theory. The existence of different laws of probability corresponding to different types of unpredictable phenomena was a revelation to Xenakis who incorporated in his music those that could govern sound characteristics. Unlike serial principles, probability theory provides a suitable means to deal with any number of sounds. Xenakis could organize them according to a given mean or density. The intervals of pitch, durations, dynamics etc. can be determined or evaluated in relation to a theoretical distribution. Xenakis elaborated on two types of stochastic music: free stochastic music, applied to the works of 1955-57; and Markovian stochastic music, applied to the works of the following two years, 1958-59.
Xenakis’s first writing on the possible applications of probability theory to organize sound characteristics dates from 1956. It includes examples dealing with speeds, durations and intervals of pitch. The first two will be examined here. The glissando plays a fundamental role in Xenakis’ music. It is likened to a straight line, the slope of which corresponds to a speed. To illustrate a possible application of probability theory to the distribution of speeds, Xenakis provided a music example taken from measures 52–59 of Pithoprakta (1955-56) accompanied by a graphic representation of the same measures drawn on graph paper.
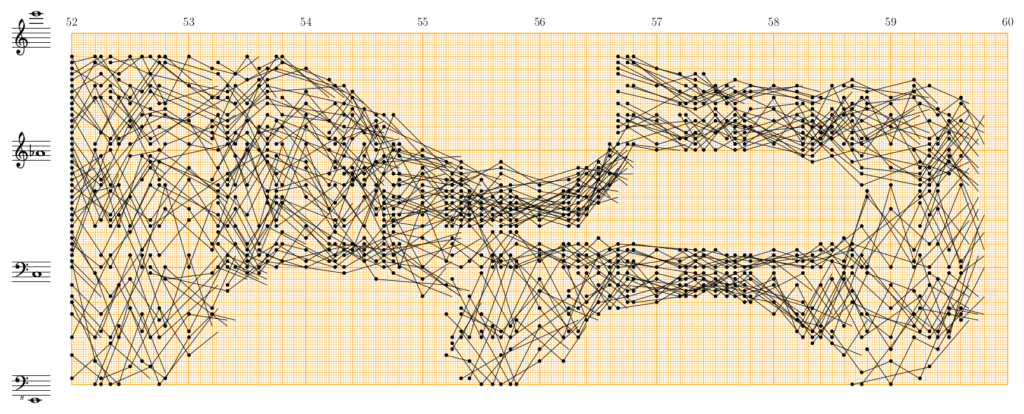
Transcription from the score: Benoît Gibson.
In this passage, each glissando is triggered by a pizzicato. The end of one glissando is not necessarily linked with the beginning of the next one. Xenakis breaks the lines in order to move them in different registers. By doing so, he takes care to indicate the string on which the glissando is played and makes sure that the next glissando starts from the same position when the player executes a string change. The overall shape of this cloud is conditioned by a constant density and the registers of the instruments. At the beginning, the glissandi fill the space within the limits of the instruments. Then Xenakis modulates the sound by filtering registral areas while densifying others. As a sculptor, he modifies the sonic qualities of the texture. But to carry out this sonic transformation, Xenakis also made some calculations. The principles on which this passage is based are described as follows:
Each of the lines represents a speed taken from the table of probabilities calculated with the formula
$$f(v) = \frac{2}{\alpha \sqrt[]\pi}e^{-(\frac{v^2}{\alpha^2})}$$
A total of 1148 speeds, distributed in 58 distinct values according to Gauss’ law, have been calculated and traced for this passage (measures 52–60, with a duration of 18.5 sec.) The distribution being Gaussian, the macroscopic configuration is a plastic modulation of the sonic material.
Xenakis 1992, 15
Fifteen years after he completed Pithoprakta, Xenakis utilized passages of glissandi from measures 52–59 in Aroura (1971). As is often the case in Xenakis’s first pieces, each instrument is assigned a metric pattern that results from the division of the basic duration into 3, 4 or 5 units. Xenakis superimposes these rhythmic values to create a sense of continuity.
In the wake of Pithoprakta, Xenakis developed the idea of total indeterminism. “What is the minimum of logical constraints necessary for the construction of a musical process?” (Xenakis 1992, 16). Chance can act as an aesthetic law, a normal philosophy (Xenakis 1992, 25). A work composed that way becomes a fragment of a stochastic distribution of sonic events. By the indeterminism of their relationships and the absence of dynamic evolution, Achorripsis (1956-57) opens up a new category later termed by Xenakis as outside-time. The work relies on the distribution of sonic events thought of independently of time. In measures 52–59 of Pithoprakta, the use of probability theory applies to one parameter only: speed of the glissandi. In Achorripsis, Xenakis extends its application to other parameters. Besides speeds, densities, intervals of durations and pitch, the whole structure of the work is based on laws of probability. To realize Achorripsis, Xenakis calculated the probability of occurrences of sonic events using the Poisson’s distribution: $$P_k = \frac{\lambda^{k}}{K!}e^{-λ}$$ with a mean density of events per unit λ = 0.6. The distribution of these events is represented by a matrix where each line corresponds to a “timbre” and each column to a unit of time.
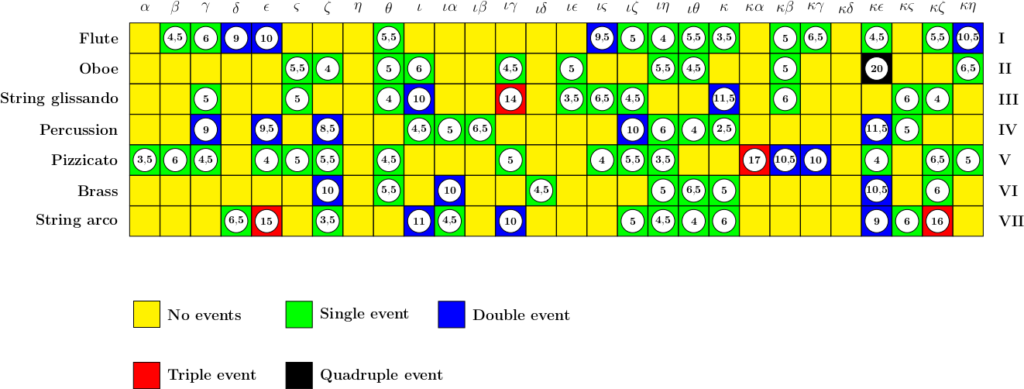
Transcription: Benoît Gibson.
Markovian stochastic music draws its inspiration from the theory of Markov chains, where the probability of each event depends only on the state of the preceding event. Although it occupies an important part of Xenakis’s theoretical writings—almost a third of the first edition of Formalized Music (Xenakis 1963, 57-131)—only three works refer explicitly to it: Analogique A, Analogique B and Syrmos. Analogique A is scored for nine string instruments: three violins, three cellos and three double basses. It was composed in 1958, in the year following the completion of Achorripsis. In Analogique A, Xenakis started from the hypothesis that all sound is an integration of grains (Xenakis 1992, 43; see also Granular Synthesis) to define a set of eight differentiated screens that he labelled (A) through (H). What Xenakis calls screens are small clouds of grains, half a measure in duration, characterized by the average densities and intensities of the sounds distributed in selected registers. The screens thus defined are outside-time. Duration is no longer a variable associated with a probability distribution. The playing techniques arco, sul ponticello, frappé col legno plus mutes are used to modify the timbral quality of the sound. As for the position of the individual grains within each register, Xenakis probably relied on his own intuition. After defining the screens, Xenakis designed a process to determine the probabilities that the screens will be transformed in other screens. If we repeat this process a number of times, the number of screens will reach fixed proportions. For instance, measures 15–30 of Analogique A contain only screens (A). At the next stage, measures 31–45, the proportion of screens will be altered to contain all screens.
The first examples of stochastic music dealt with continuous or explosive transformations of masses of sounds. These transformations occurred in-time, and depended on time. But as Xenakis went further in his attempt to formalize music, time ceased to be a criterion. For instance, in Achorripsis, the distribution of the durations are not calculated for each instrument, but in such a way that the projection of the points of departure on a straight line describes a stochastic distribution. The same goes for pitch. The distribution of intervals is not calculated within each voice but between the instruments. They are not independent lines, but a cloud of sounds conceived globally. Xenakis composed samples of sonic events defined as being outside-time. These sonic events were represented in a schema, a matrix, that admits a formal equivalence between all the occurrences of the same timbre. To some extent, rows and columns are interchangeable (Xenakis 1992, 32). The music does not follow a directional motion: it is not directed towards a goal. The same applies to Markovian stochastic music. The formal scheme of Analogique A consists of sequences of screens defined by characteristics of density, register and dynamic. These screens follow each other according to proportions inspired by the theory of Markov chains. Within a sequence, a screen is easily interchangeable with any screen of the same type.
It should be recalled that Xenakis opposed the linear conception of sound masses when he criticized what he called the “linear polyphony” of serial music, whose final result amounted to a “mass of notes in various registers” (Xenakis 1992, 8). To solve this contradiction, he composed clouds of independent sounds. What matters is the statistical mean of the sounds.
Acknowledgment
This text has been adapted from Gibson, Benoît. 2011. The Instrumental Music of Iannis Xenakis: Theory, Practice, Self-Borrowing. Iannis Xenakis Series, No. 3. Hillsdale, N.Y. : Pendragon.
References
Barthel-Calvet, Anne-Sylvie. 2003. “MÉTASTASSIS-Analyse: Un texte inédit de Iannis Xenakis sur Metastasis,” Revue de Musicologie 89/1, 129–187.
Xenakis, Iannis. 1956. “Wahrscheinlichkeitstheorie und Musik,” Gravesaner Blätter 6, 28–34.
Xenakis, Iannis. 1963. Musiques formelles, La revue musicale double numéro spéciale, 253-254, 57-131. Paris: éditions Richard-Masse.
Xenakis, Iannis. 1992. Formalized Music: Thought and Mathematics in Composition. Rev. ed. Stuyvesant, NY: Pendragon.
Xenakis, Iannis. 1994. “La crise de la musique sérielle.” In Kéleütha (Ecrits), edited by Alain Galliari, preface by Benoît Gibson, Paris: L’Arche.
How to cite
GIBSON, Benoît. 2023. “Stochastic Music.” In A Xenakis Dictionary, edited by Dimitris Exarchos. Association Les Amis de Xenakis. https://www.iannis-xenakis.org/en/stochastic-music

