James Harley
In mathematics, a random walk is a process that describes a path that consists of a succession of random steps on some mathematical space (e.g., 2-dimensional space: amplitude-time, or pitch-time). It was first introduced by Karl Pearson in 1905. An elementary example of a random walk is on the integer number line which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (known as Brownian motion – see Wikipedia).
Iannis Xenakis became interested in random walks in the 1960s, while working on a new approach to digital sound synthesis (see Stochastic synthesis). Prior to this point, he had applied stochastic processes to the creation of discrete events (notes, durations, etc. – see Xenakis 1992, 1-42). In his chapter in Formalized Music, “New Proposals in Microsound Structure,” he includes a section titled “New proposals in micro composition based on probability distributions” (Xenakis, 1971, 246-54). In this chapter, he offers some criticisms of the standard models of sound synthesis and analysis, noting the preponderance of non-harmonic, i.e. irregular waveforms, fluctuations that tend to be overlooked in the Fourier model (243-6). He proposes eight methods for stochastic synthesis, using different mathematical tools (246-9). The main focus is generating amplitude values and time-points. In both cases, the values and durations could be entirely random, or more constrained.
The work that he carried out at Indiana University did not bear much fruit in terms of direct stochastic sound synthesis (discussed in detail in Turner 2014, 102-22). But, he was able to produce some graphic outputs of waveforms based on different mathematical functions, generated by his student Cornelia Colyer (Xenakis 1992, 250-4). At the same time as they were working on this new approach to sound synthesis, it seems to have occurred to Xenakis that stochastically generated waveforms could also be mapped onto higher-order time scales, pitch-time rather than sample amplitude-time. His first effort to apply random walk output to a musical work, where the waveform was used to create a melody rather than a soundwave, was in 1971. Mikka, for solo violin, consists of a single sound unfolding continuously throughout the piece, mapping randomly generated output onto glissandi. In essence, the music is a random walk, slowed way down, where a curve that would last microseconds when applied to a synthesis model is here mapped onto a time-frame of seconds or fraction of seconds. A graphic transcription of the score demonstrates clearly how the random walk curves could produce either a score or a micro-level sound. In other words, the output from Mikka represents an interesting transferal from waveforms generated by random walk processes to music where the violin is capable of performing continuous glissandi (see figure below). While the music engages with other parameters such as dynamics, articulations, timbral shifts, the violin enables the composer to bypass the limitations of frets, keys or fingerings as would be the case with other instruments where continuously evolving pitch contours are much less possible. As a clear counter-example, the piano has no capacity to convey continuously changing pitches. Study of the Mikka score gives rise to a few observations: that the variation of time-point durations affects the shape and character of the resulting music in a fundamental way; and that the barriers of the random walk, whether they be fixed at the lowest and highest notes playable on the instrument, or whether the barriers are more elastic so that they could fluctuate between wide limits or narrow ones, also affect the results in a fundamental way.
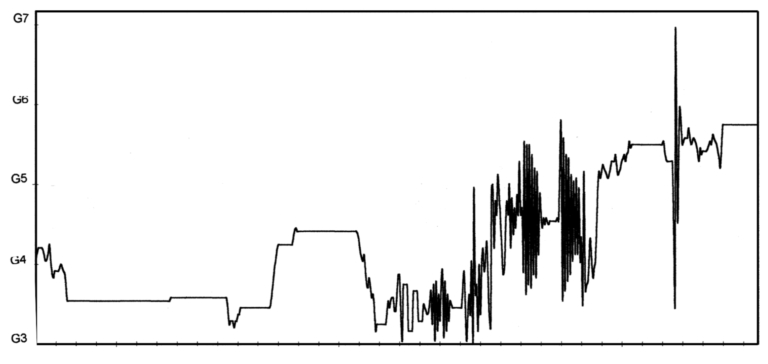
Having accomplished his adaptation of random walk output from the micro level to the instrumental (or vocal) time-scale and pitch mapping, Xenakis adopted the random walk technique to a number of other compositions. With Mikka S (1976), also for violin, he combined two lines for one instrument, which necessitated careful consideration of random walk barriers for the two parts, so that it would be physically possible to play the two at the same time. That is, the random walk pitch barriers here need to also be constrained by specific performability issues. Theory combines with practice, giving rise to new creative avenues to explore. With other works scored for more than one player, such as Noomena (1974) for orchestra or Épéi (1976) for six instruments, he was able to build complex linear musical structures generated by random walks, constrained in various ways.
One of the most important innovations Xenakis explored after the works built mainly from random-walk derived glissandi was to explore music based on a grid-like approach, where the output of the random walk is applied to discrete points. The ordering of one note to the next could be generated by random walk procedures, but the texture can move away from radical linearity as in Mikka to other structures. He explored random walks applied to a 2-dimensional grid (pitch-pulse) in a number of works, notably in Evryali (1973) for solo piano. Here, the random walks are constrained in a number of ways, but the basic point of departure is the chromatic set of pitches, a fixed tempo, and a consistent division of beats into four.
In addition to creating a grid of set points rather than connecting continuously fluctuating waveforms, Xenakis also begins exploring pitch grids generated by sieves, or non-uniform values; in other words, specific pitch sets (sieves) rather than the uniform chromatic complement (see Sieve theory). A clear example of combining constrained random walks with pitch sieves is the opening section of Jonchaies (1977) for orchestra, where a held note in the strings turns into a quasi-modal melody, proliferating into a bundle of six melodies. The material here is not constrained by the physical limitations of performing two lines by one player, but there is an overall elastic barrier applied that produces a composite wave shape from the six lines.
Once Xenakis began creating complex textures built from random walks involving two or more lines simultaneously, he was able to incorporate random walks with other formal models. Perhaps the most closely connected technique he explored was a contrapuntal bundling of simultaneous lines into what he called arborescences. Evryali is one of the first works to explore this technique. This approach involves using other mathematical tools, such as topological transformations, to create variations of what may have originally been random-walk contours, enabling related lines to be drawn into complex musical textures that he was able to create from these mathematical tools. In addition to Jonchaies, Xenakis explored arborescence textures in numerous works, such as Mists (1980) for solo piano, where there are up to four simultaneous lines, or Erikhthon (1974) for piano and orchestra, where graphic sketches show how designs proliferate in ways that combine random walks with transformational techniques, and sieves (pitch and rhythm).
References
Harley, James. 2004. Xenakis: His Life in Music. New York: Routledge.
Turner, Charles W. 2014. Xenakis in America. New York: One Bock Avenue.
Wikipedia, The Free Encyclopedia. s.v. “Brownian motion,” last modified 9 September 2023 21:30 UTC, https://en.wikipedia.org/wiki/Brownian_motion
Xenakis, Iannis. 1971. Formalized Music: Thought and Mathematics in Composition, translated by Christopher Butchers, G. W. Hopkins, and Mr. and Mrs. John Challifour. Bloomington and London: Indiana University Press.
Xenakis, Iannis. 1992. Formalized Music: Thought and Mathematics in Composition. Rev. ed. Stuyvesant, NY: Pendragon Press.
How to cite
HARLEY, James. 2023. “Random Walk.” In A Xenakis Dictionary, edited by Dimitris Exarchos. https://www.iannis-xenakis.org/en/random-walk/
