James Harley
The concept and technique of arborescence came to Iannis Xenakis after he had written and published his important texts about his music. He began working with it in the early 1970s, about the same time as Formalized Music was published in its English, expanded form (Xenakis 1971). Regrettably, he does not mention it there. In latent form, Xenakis may have been thinking about arborescence while working on Synaphaï (1969) for piano and orchestra. This work explores what he calls connexities (see preface to the score), and the linear writing for the soloist even goes as far as notating separate staves for each finger. His most detailed discussion of arborescence is found in the book of interviews with Bálint András Varga. Published in 1996, the book is based on conversations held in 1980 and 1989. There, his explanation begins with the notion of a point. In time, a point repeats itself to assert its presence, forming a line. The values that make up this line could conceivably change, possibly as the result of random walk activity, the most basic form of which involves selecting randomly a neighbour value. In other words, if the point value is set at zero, then neighbour values would be 1 or -1. With the possibility of the value of the point-line changing, different paths can result. More sophisticated random processes, based on stochastic mathematical functions, will produce more variable outcomes, even acting on a simple starting point. A line (trunk) can generate a tree-like structure as a result of iterative runs of the generative process. As Xenakis puts it,
starting out at a point we have reached a bush or even a tree. This can occur freely but also according to rules and can become as complicated as lightning or the veins of the body.
Varga 1996, 88
Xenakis developed a theoretical foundation for this approach, no doubt owing to his training as an engineer (although he did not publish an extensive treatment of arborescences). One concept he drew on relates to topological transformations. This is described as
continuous transformation, […] or homeomorphism, […] a one-to-one correspondence between the points of one figure and the points of another figure such that points that are arbitrarily close on one figure are transformed into points that are also arbitrarily close on the other figure.
The Columbia Electronic Encyclopedia, “Topology: Continuous Transformations and Equivalent Figures”
Random walks and topological transformations provided foundations for the technique of arborescence. A great deal of Xenakis’s work, though, was carried out through graphic sketching and design, later transferred into sound. It should be noted that his work on arborescence took place around the same time as he was developing his graphic computer music system, the UPIC, which was unveiled in 1978. The UPIC enabled the user to draw sounds as graphics that are better rendered into sound directly, without the need for musical notation.
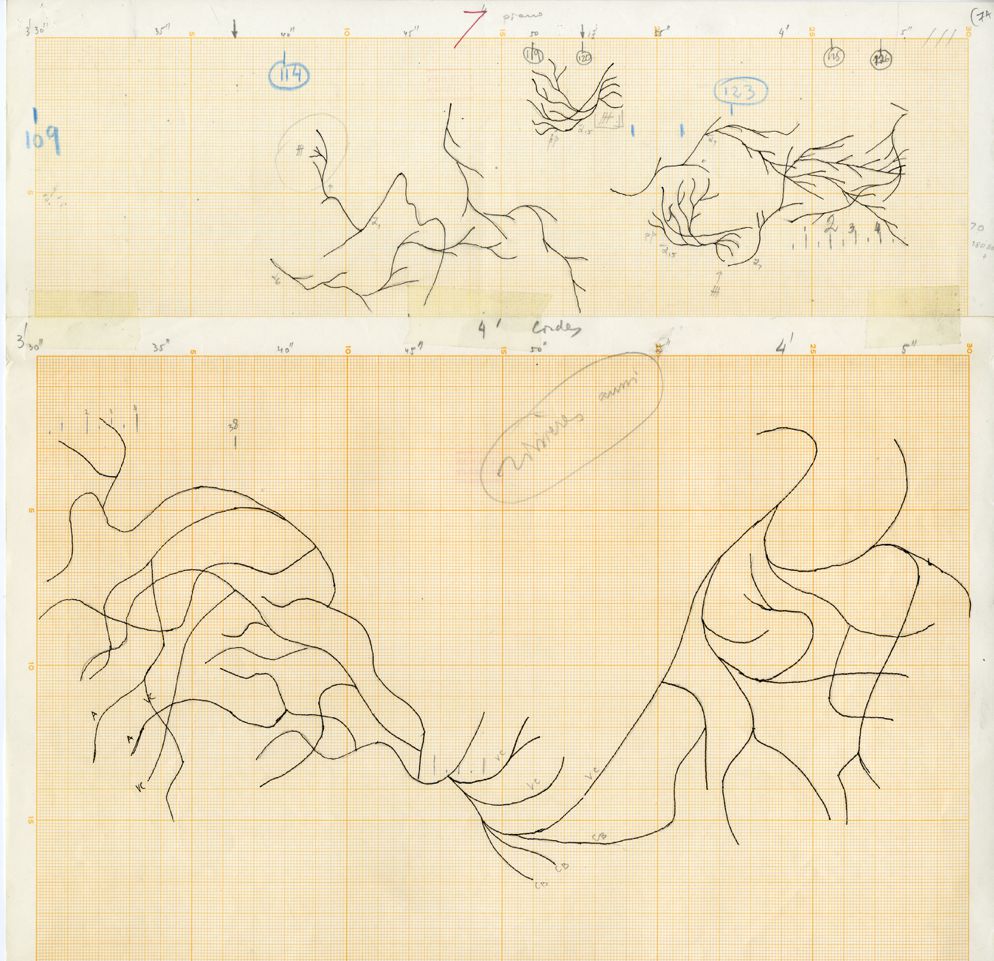
For Erikhthon (1974) for piano and orchestra, Xenakis created a number of graphic sketches that he then transcribed into music. This example clearly indicates tree-like shapes; one of them has been replicated a number of times, each instance being placed at a different angle and location. The organization of the design is clearly apparent when viewing, but it may be more difficult to perceive sonically. This is because the transferal into sound maps pitches on the vertical axis, and time onto the horizontal axis. In some cases, the arborescence may produce chords rather than melodies, because of the way the design maps into the pitch-time space. In a way, the composer is challenging us, the listeners, to learn to recognize the identities of the shapes in sound. This is related to the more traditional notion of recognizing a melody that has been inverted, or presented in retrograde. The other interesting sonic transferal issue arises from the way that the designs are transcribed into music. For string instruments, in this case drawn from the orchestra, the designs can be translated into sound by means of continuous glissandi. For the solo piano, the shapes must be mapped onto a grid, with the continuous design being sampled at the resolution of the chromatic notes of the piano, or the temporal divisions of time represented by beats and their divisions.
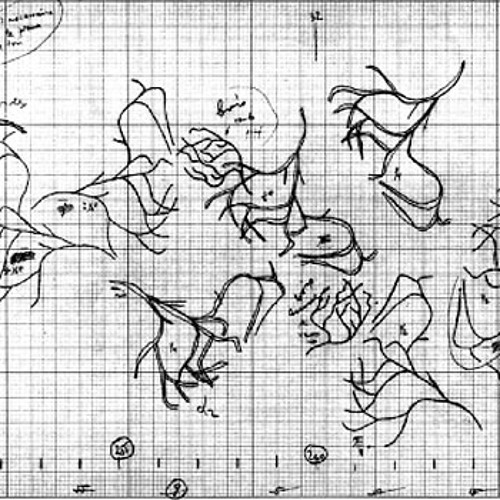
In this graphic transcription from Evryali (1973) for solo piano, the design shows how a single line can proliferate, producing as many as six independent lines. These could have been produced by applying a constrained random-walk mathematical process, or a graphic sketch. Either way, the result is a new form of counterpoint, a means of creating linear musical textures.
Xenakis drew on arborescences, proliferating linear shapes, in numerous subsequent works, including Jonchaies (1977) for orchestra, Mists (1980) for solo piano, and Tetras (1983) for string quartet. According to the composer,
the idea of arborescence is closely linked to causality, repetition and consequently variation.
Varga 1996, 88
It is therefore connected to the idea of continuity, linear motion and growth; the continuation of a generative idea is fundamentally based on aspects of its current state that take life through asserting its existence in time and evolving through stochastic principles or by intuition-design.
References
The Columbia Electronic Encyclopedia, 6th ed. (2023), Columbia University Press, s.v. “Topology: Continuous Transformations and Equivalent Figures,” https://www.infoplease.com/encyclopedia/science/math/basics/topology/continuous-transformations-and-equivalent-figures
Harley, James. 2004. Xenakis: His Life in Music. New York: Routledge.
Varga, Bálint András. 1996. Conversations with Iannis Xenakis, London: Faber and Faber.
Xenakis, Iannis. 1971. Formalized Music, Bloomington, Indiana University Press.
How to cite
HARLEY, James. 2023. “Arboresence.” In A Xenakis Dictionary, edited by Dimitris Exarchos. Association Les Amis de Xenakis. https://www.iannis-xenakis.org/en/arborescence