Benoît Gibson
Xenakis refers to group theory mainly in two different contexts. On the one hand, to demonstrate the ordered structure of sound characteristics—this allows him to establish a correspondence between numbers and pitch; on the other hand, to explore the symmetries proper to the structures of finite groups. Xenakis utilizes systems of group symmetries for the first time in Akrata (1964), at the time when he developed the notions of outside-time, temporal and in-time with respect to “Symbolic Music” (Xenakis 1992, 155-77). Recourse to group theory marks a new direction in Xenakis’s approach to composition. While stochastic music relies on indeterminism, group structures organize predetermined elements according to a specific order.
A group G is defined as a set of elements for which a single law of composition satisfies the following conditions (see Ledermann 1964, 2):
- Closure: to every ordered pair of elements A, B of G there belongs a unique element C of G, written C = A∗B, which is called the product of A and B.
- Associative law: if A, B, C are any three elements of G, which need not be distinct, then (A∗B)∗C = A∗(B∗C) so that either side may be denoted by A∗B∗C.
- Unit element: G contains an element I, called the unit element or identity such that for every element A of G A∗I = I∗A = A.
- Inverse element: corresponding to every element A of G, there exists in G an element A−1 such that A ∗ A−1 = A−1∗A = I.
As is often the case, Xenakis seeks to subsume existing compositional procedures under broader or more abstract categories. It is therefore not surprising that he refers to a set containing the four melodic forms (prime (P), retrograde (R), inversion (I), inverted retrograde (IR)) as an example of group structure (Xenakis 1990, 17-18). The product of any two forms produces a form of the group (closure). The prime form (P) of any other transformation leaves it unaltered. It corresponds to the unit element: the product (P∗IR), as the product (IR∗P), is equal to (IR). Each form is its own inverse: the products (P∗P), (R∗R), (I∗I) and (IR∗IR) all yield the prime form (P) (unit element). Finally, the four transformations of a melodic line satisfy associative law: ((P∗R) ∗ IR) = (P∗(R∗IR)) = (I).
The order of a group corresponds to the number of its elements. The melodic forms (P), (R), (I) and (IR) constitute a group of order 4, known as the Klein four-group. For a group of order 4, there are 16 distinct products, which can be set out in a multiplication table (matrix) where each element is assigned a column and a line.
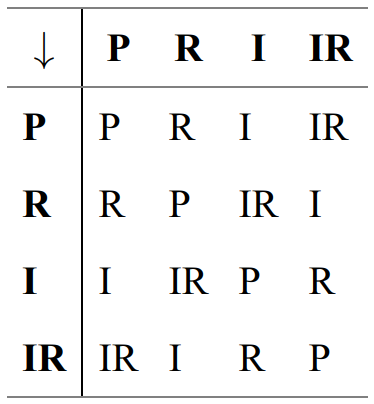
The result of the product of two elements stands at the intersection of the corresponding column and line: (R∗IR) → (I). It would be possible to form a larger group of order 48 by adding 12 transpositions to each form. The transpositions would add up as indices of moduli 12. Thus, the product of transformations (IR7) and (I5) would equate (R0): (IR∗I = R) and (7 + 5) = 12 (mod 12) = 0.
Xenakis uses melodic figures that he treats as elements of group structures in Nomos Gamma (1967).

Excerpt from Nomos Gamma (1967), mm. 203–205
The melodic figures played by the oboes in mm. 203-205 rely on the following series of intervals of pitch in quarter-tones:
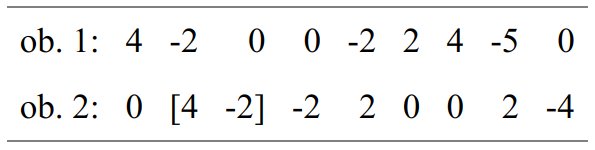
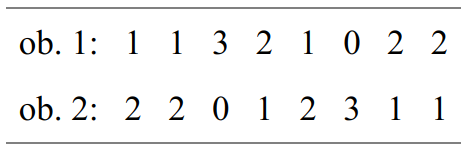
Leaving aside a deviation at the beginning (shown in brackets), the line of the second oboe follows the inverted retrograde form of the series of intervals of the first oboe. The same applies to the dynamic profiles. The dynamic contour of the second oboe is an inverted retrograde form of the dynamic contour of the first. As for durations and playing techniques (stacc., flatt., quilisma), they appear in retrograde. However, the unit durations are different: quintuplet eighth notes for the first oboe versus eighth notes for the second:
Geometric shapes or figures can be organized according to the principles of abstract groups. But in Xenakis’s work, the use of group theory serves mainly to structure cycles of permutations. Much of what we know about Xenakis’s use of group structures comes from the composer’s own analysis of Nomos Alpha (1965-1966) (Xenakis 1992, 215-36). Permutations are transformation processes denoted by an ordered series of integers. Each integer is determined by the position it occupies within a set of elements and by its numerical value. The permutation (1324) disposes the elements in the order indicated in parentheses, whatever their values. Applied to the set {bdce}, it produces a new set where the elements appear in the following order: {bcde}.The permutation notated as (1234) maintains the order of the elements unchanged. Within a group structure, it stands for the unit element (identity).
The number of different ways in which n elements can be ordered is equal to factorial n (n! = 1 × 2 × 3 × … (n − 1) × n). The set of these permutations forms a group. Their number (n!) is the order of the group. The matrix below reproduces the matrix of a group isomorphic with the rotations of a cube around its symmetry axes, as provided by Xenakis in his article “Towards a Philosophy of Music” (1992, 221).
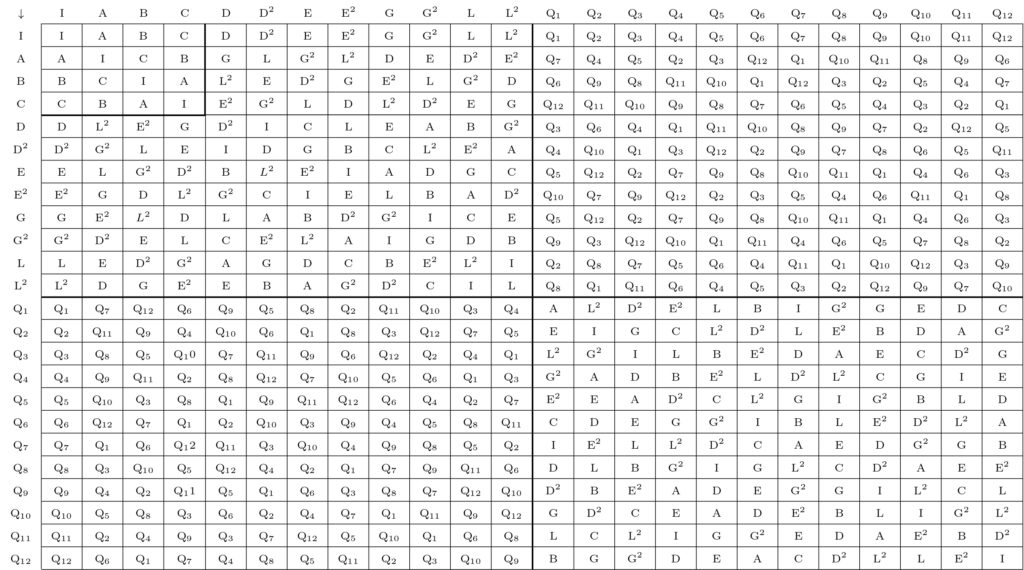
Matrix of the symmetric group P4
This group permutates eight elements that can be regarded as the eight vertices of a cube. The following table lists the symbols associated with each permutation.
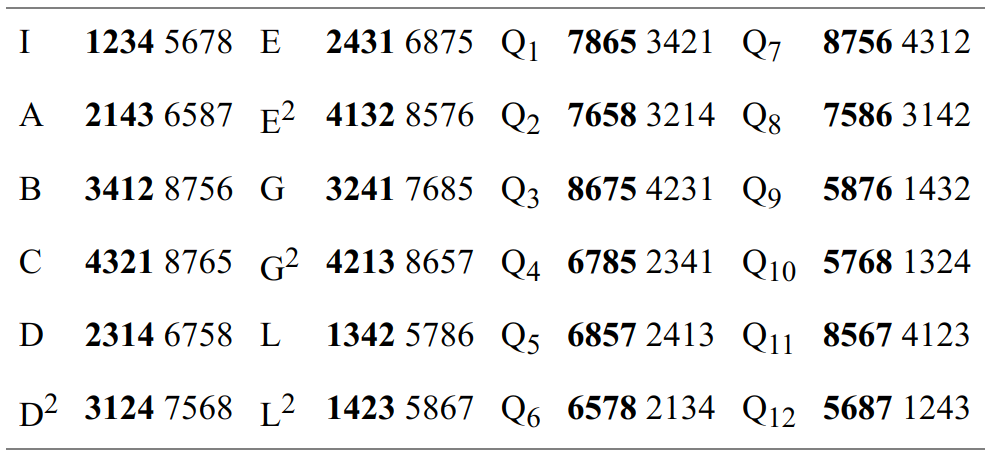
As for the preceding matrix, the result of any two transformations is found at the intersection of a column and the corresponding line. The product of transformations (D) and (A) is (G): (D∗A) → (G). One should notice that this group is not commutative: (D∗A) ≠ (A∗D).
The group which consists of the rotations of a cube around its symmetry axes is isomorphic with permutation group P4 , that is, the group that contains all permutations of four elements. The order in which the matrix displays the transformations also shows two sub-groups. The first, formed by transformations {I, A, B, C}, is isomorphic with the Klein four-group. A correspondence can be established between the groups {I, A, B, C} and {P, R, I, IR}. They have the same structure and differ only with respect to notation. The second sub-group gathers transformations (I) to (L2 ). It is also known as the alternating group A4
Group theory helped Xenakis organize cycles of permutations according to a system. It led to a structuring of sound characteristics similar to that produced by sieve theory. But whereas sieve theory is based on one dimension, in most cases, the pitch or time axis, permutation groups unfold in two dimensions: an outside-time structure that defines the elements of a group, and a temporal, kinematic structure that determines the ordered succession of the elements. Once the elements of a permutation group have been defined, Xenakis then applied the permutations cyclically according to a simple rule. In most cases, the transformations follow one another so that the following transformation (permutation) is the result of the two preceding ones. For instance, within the permutation group P4, following transformations (A) and (D) comes transformation (L2), then (E), (C), etc. This procedure generates series of cyclic paths. With regards to the permutation group P4, there are 70 different paths that can be classified into 12 classes of different order. The beginning of the path can occur at any point.
Acknowledgment
This text has been adapted from Gibson, Benoît. 2011. The Instrumental Music of Iannis Xenakis: Theory, Practice, Self-Borrowing. Iannis Xenakis Series, No. 3. Hillsdale, N.Y. : Pendragon.
References
- Ledermann, Walter. 1964. Introduction to the Theory of Finite Groups. Edinburgh and London: Oliver and Boyd.
- Xenakis, Iannis. 1990. “Originality in Musical Composition.” IN Technology’s Challenge for Mankind, edited by the Steering Committee of the Fukushima International Seminar, Tokyo: Technova.
- Xenakis, Iannis. 1992. Formalized Music. Thoughts and Mathematics in Music. Hillsdale, New York: Pendragon.
How to cite
GIBSON, Benoît. 2023. “Group Theory.” In A Xenakis Dictionary, edited by Dimitris Exarchos. Association Les Amis de Xenakis. https://www.iannis-xenakis.org/en/group-theory
