Peter Hoffmann
A cellular automaton (CA) governs, among others, only a few bars in Horos (1986) and, through an act of self-borrowing, in Ata (1987) (see Solomos 2006); however, this late example of a musical appropriation of a scientific model is particularly telling for Xenakis’s passion for science, mathematics and computation on the one hand and his compositional practice on the other.
It is more or less certain that Xenakis was inspired by a seminal article about cellular automata by Stephen Wolfram (the author of Mathematica, a software that is used by almost every mathematician or physicist in the world) in the popular periodical Scientific American (Wolfram 1984). Xenakis chose a CA of class 3, as presented by Wolfram. Class 3 cellular automata are considered by Wolfram as capable of modeling dynamic systems, turbulence and chaos, and that is exactly what Xenakis was interested in. Wolfram defines, in his article, three more classes of cellular automata: CAs of class 1 all end up in a fixed state, regardless of their starting state; all class 2 CAs end up in a pattern of periodically repeating states; finally, class 4 CAs are capable of universal computation and as such are able to model our entire universe as a giant self-computing machine.
But what is a cellular automaton, in the first place? Xenakis used the following words in order to describe this:
Let’s say you have a grid […] with […] small squares, that is, cells. These are empty. It’s for the composer to fill them. How? […] You start at a given [cell] and you say here is a note played by an assigned instrument. What’s the next moment going to be? What notes? In accordance to your [CA] rule, the cell which has been filled gives birth to, say, […] two adjacent cells. In the next step each cell will create […] two other notes. Your rule helps to fill the entire grid.
Varga 1996, 199-200
By “grid,” Xenakis refers to musical space-time (the evolution of pitch over time). That is to say, Xenakis uses a one-dimensional CA where cells are strung on a line, as the vertical dimension of pitch, which, in the case of Horos, is sieved (mm. 10 and 14-18) (see Sieve Theory). For each cell of the next time slice (the vertical line of cells to the right, i.e. the next chord) the CA rule determines its pitch as a function of its current state and that of its two adjacent cells. There are four instrumental colors: 0 for mute, 1 for brass, 2 for woodwind, and 4 for strings. The value of a cell is equal to the value of the cell at the previous time slice plus the values of its two adjacent cells. This sum is then transformed according to the code 4200410, read from right to left, where the sequential positions represent the sums of 0, 1, 2, etc. and the number stands for the value of the cell to be computed (0 → 0, 1 → 1, 2 → 4, 3 → 0, and so on) (see Solomos 2006).
Xenakis’s CA rule, therefore, preserves silence over time, but when being adjacent to a brass sound, the brass is propagated across the scale of pitches (see figure below). Therefore, a “seed” of an igniting brass note simultaneously creates an ascending and a descending branch of brass notes over the sieve. The cells (pitches) in between are filled with other instrumental sounds (or mutes) according to the CA rule. In other words, the CA unfolds an ever bigger orchestral tutti cluster reaching out to the tuba at the low end and high string notes at the high end. When blended onto an equidistant structure (such as the pixels of a computer screen), the CA’s evolution in time leaves the trace of a fractal structure, a so-called Sierpinsky triangle.
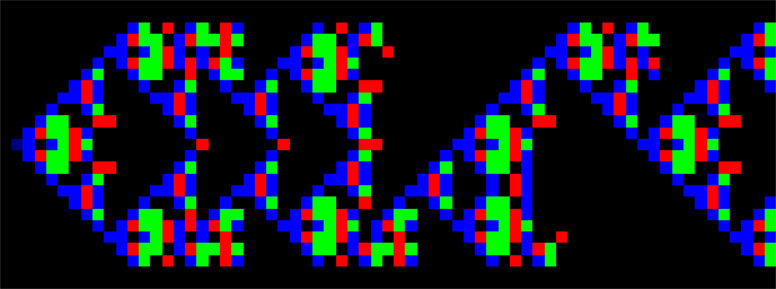
Xenakis enlarged Wolfram’s rule in order to accommodate the strings as an additional color of his orchestra. He also interfered with the CA in other ways. In Horos, once the orchestra cluster has spread over the entire ambitus of available pitch, Xenakis changes the value of some notes and as a result, the upper CA branch dies out. In what follows, the CA grows back from below, until it covers the entire ambitus again. Just before the CA enters a repetition loop (due to its limited ambitus), Xenakis switches it off. At another instance Xenakis breaks the process and interpolates 3 measures of music that have nothing to do with the automaton. We also see that Xenakis combines regular meter in the first half of his CA with irregular, probably sieved meter in the second half. It is as if Xenakis was playing with the CA as the master of the game.
One year later, in Ata (1987), Xenakis reuses parts of the Horos automaton. He reproduces mm. 10, 14, 16, and 17 as mm. 126, 121, 130, and 128, respectively. However, he inverts three measures in time (i.e. retrograde versions of mm. 126, 121, and 128). This is particularly interesting from a theoretical point of view. The CA of Horos and Ata is a discrete dynamic system modeling an irreversible flow or a diffusion process. As three predecessor values are mapped onto a single successor value, the rule entails some loss of information and is therefore not reversible in time. When Xenakis declared that “indeed, much like a god, a composer may create the reversibility of the phenomena of masses, and apparently, invert Eddington’s ‘arrow of time'” (Xenakis 1992, 255), he could actually be referring to an example like this.
With his CA, Xenakis bends a scientific model (later to be claimed by Wolfram to be the Holy Grail of a Theory of Everything, as commented in Becker 2020) to fit in his musical universe.
References
Becker, Adam. 2020. “Physicists Criticize Stephen Wolfram’s ‘Theory of Everything’.” Scientific American. Accessed May 24, 2022. https://www.scientificamerican.com/article/physicists-criticize-stephen-wolframs-theory-of-everything/.
Hoffmann, Peter. 2002. “Towards an ‘Automated Art’: Algorithmic Processes in Xenakis’ Compositions.” Contemporary Music Review 21 (2–3): 121–31. https://doi.org/10.1080/07494460216650.
Solomos, Makis. 2006. “Cellular Automata in Xenakis’s Music. Theory and Practice.” In Definitive Proceedings of the “International Symposium Iannis Xenakis” (Athens, May 2005). https://cicm.univ-paris8.fr/ColloqueXenakis/papers/Solomos.pdf.
Varga, Bálint András. 1996. Conversations with Iannis Xenakis. London: Faber and Faber.
Wolfram, Steven. 1984. “Computer Software in Science and Mathematics,” Scientific American vol. 251, no. 3, pp. 188-203.
Xenakis, Iannis. 1992. Formalized Music: Thought and Mathematics in Composition / Iannis Xenakis. Rev. ed., additional material compiled and edited by Sharon Kanach, Stuyvesant, NY: Pendragon Press.
How to cite
HOFFMANN, Peter. 2023. “Cellular Automata.” In A Xenakis Dictionary, edited by Dimitris Exarchos. Association Les Amis de Xenakis. https://www.iannis-xenakis.org/en/cellular-automata
